Electronics Lessons: Making Gates from Gates

The most useful logic component that you'll ever find. -the NAND Gate.

So I've looked at logic gates and said that there are three Basic ones, AND, OR, NOT, that there is also an exclusive OR XOR, and that on top of that there is XNOR and NAND that can be made by adding a not gate to the end of the outputs.

We've had a peek at boolean algebra to show how things can be proven algebraically, and looked at truth tables to give a much more show and tell approach to showing binary states and logical outputs.

So now we'll look at how you can make any logic gate from a NAND gate.

We'll start by looking at the truth table for the NAND Gate

A B | Q
======
0 0 | 1
0 1 | 1
1 0 | 1
1 1 | 0

NOT
So lets start with the simplest functions.

Imagine that we connect both inputs together, so that inputs A and B are both the same,
now we're only concerned with states 0 and 3 on the truth table.

A B | Q
======
0 0 | 1
1 1 | 0

And it's only really a single input,

A | Q
====
0 | 1
1 | 0

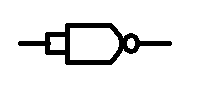
Connecting both inputs of the NAND gate has made the NAND gate into a NOT gate.

AND
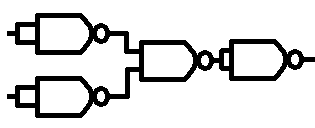
So how do we make a NAND gate an AND gate

A . B = //(A . B)
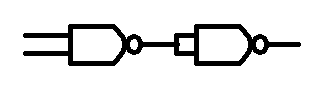
A . B = NOT NOT A AND B

yep, we just have the output of a two input NAND gate, connected to both inputs of a second two input NAND gate.

OR

Lets start with a truth table

A B | A + B | /A /B | /(/A . /B)
=======================
0 0 |    0    |  1  1  |    0
0 1 |    1    |  1  0  |    1
1 0 |    1    |  0  1  |    1
1 1 |    1    |  0  0  |    1

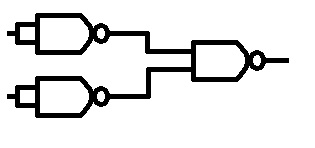
So first we make a couple of not gates, just like above, then we feed those to a NAND gate.

XOR
So we have our basic NOT, OR, AND gates all figured out, there is also the NAND gate already given (as that's out basic construction block)

Now we're going to look at XOR

To understand what XOR is I'll put the term into English.

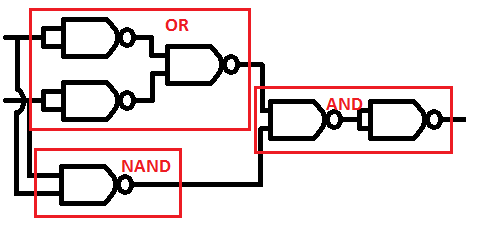
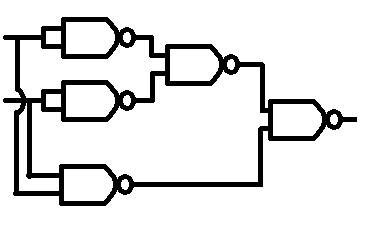
XOR is, A or B, but not A and B

(A + B) . /(A . B)
Let's draw up the truth table for that one.


A B | XOR | OR | NAND | OR AND NAND
================================
0 0 |    0    |  0  |     1    |          0
0 1 |    1    |  1  |     1    |          1
1 0 |    1    |  1  |     1    |          1
1 1 |    0    |  1  |     0    |          0

XNOR

We can create an XNOR gate by adding a not gate to the end of our XOR gate, but Given that the last element is already a NOT gate, (NAND with conjoined inputs) rather than having two not gates back to back we can just remove the not gate already there.

NOR
And of course the NOR gate is just the OR gate with a NOT gate added to the end.