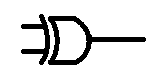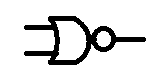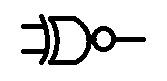Electronics Lessons: Logic Notation

In the last post I looked at various gates.

Now we're going to look at the various notations that are used when writing out statements of what logic circuits do.

First, lets think about a binary circuit.

Basically we'll have at least one input, and at least one output.

We'll call our inputs a series of letters, starting with A, and out outputs will be assigned the letter Q, if there is more than one output we'll call it Q1 and Q2.

It's exactly the same notiation for all the logic operators if you call inputs In1, In2 and so on


So lets start with the four simple gates
NOT, AND, OR, XOR
/ . + ⊕

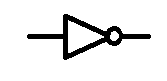
the NOT gate is a slash.

Q = /A
q = not A

Alternativly not can be represented by an apostraphy after the letter

Q = A'
1 = 0'
0 = 1'
1 = /0
0 = /1

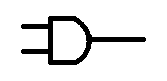
The AND gate is represented by a dot.
Q = A.B

0 . 0 = 0
0 . 1 = 0
1 . 0 = 0
1 . 1 = 1

the OR gate is represented by a plus sign.

Q = A+B
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1

and XOR is represented by a plus with a circle around it

Q = A⊕B
0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
0 ⊕ 0 = 0

finally we make up logical expressions the same way as we made up the gates for more complicated gates.
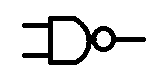
a NAND gate was just an AND gate with a NOT gate following it.

Q' = A + B
/Q = A + B
Q = /(A + B)

NOR
Q' = A+B
/Q = A+B
Q = /(A+B)

XNOR
Q' = A⊕B
/Q = A⊕B
Q = /(A⊕B)

Electronics lessons: Logic gates

Logic gates are useful in digital electronics, in digital electronics there are generally no wave forms, there is two states, either logic high or logic low, on or off, 1 of 0.

when we work with binary data we have to have a way to deal with it.

that way of dealing with it is with the use of logic gates.

There are a few basic logic gates.

NOT, AND OR, and XOR.

First NOT
You have two basic states in binary, on or off, if it's not on, it's off, if it's not off, it's on.

the not gate works in the same way as that sentence,

if you put a 1 into a not gate, it's output is 0
if you put a 0 into a not gate, it's output is 1

A | Q
====
0 | 1
1 | 0

AND

The AND gate has two inputs and one output. for the output to be on, ALL inputs to the AND gate must be on, if either one of the inputs is low then the output will also be low.

Think of it like two switches in series, both switches must be on in order for it to work.

A B | Q
======
0 0 | 0
0 1 | 0
1 0 | 0
1 1 | 1

OR

Another basic logic gate is the OR gate. again this gate has two inputs, the out put will be on  if either input A OR input B is on.

A B | Q
======
0 0 | 0
0 1 | 1
1 0 | 1
1 1 | 1

XOR
The last basic logic gate is the exclusive OR gate, XOR
With this gate the output will be on if In put A is high, OR if input B is on, but not if input A and input B is on. it must be exclusively A or B that is on, but definitely not A and B.

A B | Q
======
0 0 | 0
0 1 | 1
1 0 | 1
1 1 | 0


After this we start adding gates together to make more complicated logic gates.

if we put a NOT gate after a AND gate we make a NAND gate we invert the input of a regular AND gate.

A B | Q
======
0 0 | 1
0 1 | 1
1 0 | 1
1 1 | 0

similarly we can make a NOR gate

A B | Q
======
0 0 | 1
0 1 | 0
1 0 | 0
1 1 | 0


finally we have the Exclusive NOR gate XNOR

A B | Q
======
0 0 | 1
0 1 | 0
1 0 | 0
1 1 | 1

Counting in different bases.

This is going to be a pretty short post, to introduce a concept that will be needed in future.
That concept is binary.

The first thing to think about is that when we count, using Arabic numerals we have ten symbols.
So we could in base ten, (Decimal)

Counting works in a really simple way, we start with our lowest value symbol, and cycle through our symbols until we get to the end of the set, then we start again at the beginning putting the first symbol in our set in front of the least significant number.

most significant, digit digit digit. least significant.

to a number 10,001

The most significant part is the ten thousand, the least significant part is one.

so counting, our numerals are
0,1,2,3,4,5,6,7,8,9

when we hit nine we put our second lowest value numeral to the left in the most significant space and then cycle through numerals again.
we use the second lowest, because our lowest is 0.
000012 is the same as 12

10,11,12,13,14,15,16,17,18,19 ... 101,102,103 .... etc and so on.

Base 2
in base 2 we only use two numerals, 0 and 1

so we start with 0, our next numeral is 1.
then we've exhausted out numerals and have to put our second lowest value to the left, and cycle through, we do this again and again again again:

0, 1, 10,  11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 and so on.

Base 8
In base 8 we have 8 symbols
0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16 ,17, 20, 21, 22, 23, 24, 25, 26, 27, 30

Base 16
In base 16 we use 16 symbols, these are
0,1,2,3,4,5,6,7,8,9,a,b,c,d,e,f

so we count in the following way.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, a, b, c, d, e, f, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1a, 1b, 1c, 1d, 1e, 1f, 20, 21 and so on...

Counting from 0 to 63 the various numbers look the following way.


Decimal   Binary                   Octal        Hexadecimal
0              000000                    00                      00
1              000001                     01                     01
2              000010                     02                     02
3              000011                     03                     03
4              000100                     04                     04
5              000101                     05                     05
6              000110                     06                     06
7              000111                     07                     07
8              001000                     10                     08
9              001001                     11                     09
10             001010                     12                     0a
11             001011                     13                     0b
12             001100                     14                     0c
13             001101                     15                     0d
14             001110                     16                     0e
15             001111                     17                     0f
16             010000                     20                     10
17             010001                     21                     11
18             010010                     22                     12
19             010011                     23                     13
20             010100                     24                     14
21             010101                     25                     15
22             010110                     26                     16
23             010111                     27                     17
24             011000                     30                     18
25             011001                     31                     19
26             011010                     32                     1a
27             011011                     33                     1b
28             011100                     34                     1c
29             011101                     35                     1d
30             011110                     36                     1e
31             011111                     37                     1f
32             100000                     40                     20
33             100001                     41                     21
34             100010                     42                     22
35             100011                     43                     23
36             100100                     44                     24
37             100101                     45                     25
38             100110                     46                     26
39             100111                     47                     27
40             101000                     50                     28
41             101001                     51                     29
42             101010                     52                     2a
43             101011                     53                     2b
44             101100                     54                     2c
45             101101                     55                     2d
46             101110                     56                     2e
47             101111                     57                     2f
48             110000                     60                     30
49             110001                     61                     31
50             110010                     62                     32
51             110011                     63                     33
52             110100                     64                     34
53             110101                     65                     35
54             110110                     66                     36
55             110111                     67                      37
56             111000                     70                     38
57             111001                     71                     39
58             111010                     72                     3a
59             111011                     73                     3b
60             111100                     74                     3c
61             111101                     75                     3d
62             111110                     76                     3e
63             111111                     77                     3f

Coding Lessons: Structs (Lessons 18)

So we've dealt with Arrays and strings and passing arrays and fields to and from functions.

Now we're going to look at structured data.

Structured data is basically a list of fields, those fields can have any type, the total memory for that block is then the combined memory requirements of all the little bits of data inside that structured data block.

You can think of a struct like a row of a table.
Where we can give that table row or block of data a name.

It's probably best to write out some code and explain what's going on.

to start with structured data is created with the keyword struct.

struct product

Here we're going to create a structured data type called product, inside this data type will be a product name and a product price.
The data types that are contained in the struct declaration then follow inside curly brackets.

struct product {
float price;
int stocklevel;
};

So that's our definition of our structured data set-up.

we do this using the struct keyword again, then the name of the struct that we're referring to, (because we could define multiple struct types) then what we want to call it.

struct product apples;

now we want to poke some data into the struct, and read some data out of it:

apples.price = 0.49;
apples.stocklevel= 12;

printf("You have a stock of %d apple(s) costing $%.2f", apples.stocklevel, apples.price);


#include<stdio.h>

int main()
{
struct product { float price; int stocklevel; };
struct product apples;
apples.price = 0.49;
apples.stocklevel= 12;

printf("You have a stock of %d apple(s) costing $%.2f", apples.stocklevel, apples.price);

}